Kongruensseista
Merkintä a 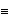 b (mod p)
tarkoittaa, että p on a - b:n tekijä.
(Merkitään p | a - b.) Toisin sanoen, kun a tai b jaetaan p:llä;, saadaan sama
jakojäännös. Seuraavat alkeelliset laskusäännöt ovat voimassa (a,b mielivaltaisia kokonaislukuja, p > 0):
b (mod p)
tarkoittaa, että p on a - b:n tekijä.
(Merkitään p | a - b.) Toisin sanoen, kun a tai b jaetaan p:llä;, saadaan sama
jakojäännös. Seuraavat alkeelliset laskusäännöt ovat voimassa (a,b mielivaltaisia kokonaislukuja, p > 0):
-
a
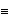 a (mod p).
a (mod p).
-
Jos a
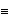 b (mod p ), niin b
b (mod p ), niin b 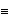 a (mod p).
a (mod p).
-
Jos a
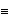 b (mod p ) ja b
b (mod p ) ja b
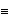 c (mod p ), niin a
c (mod p ), niin a
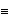 c (mod p ).
c (mod p ).
-
Jos a
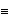 b (mod p) ja c
b (mod p) ja c 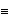 d (mod p), niin a + b
d (mod p), niin a + b 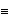 c + d
(mod p) ja ab
c + d
(mod p) ja ab 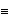 cd (mod p). Yleensäkin ekvivalenssirelaatiota ~, joka toteuttaa ehdon x R
y, x ~ u, y ~ v
cd (mod p). Yleensäkin ekvivalenssirelaatiota ~, joka toteuttaa ehdon x R
y, x ~ u, y ~ v 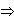 u R v sanotaan
kongruenssirelaatioksi relaatiolle R. Niinpä
u R v sanotaan
kongruenssirelaatioksi relaatiolle R. Niinpä 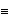 on kongruenssirelaatio yhteen- ja
kertolaskulle.
on kongruenssirelaatio yhteen- ja
kertolaskulle.
Se siitä. Vielä yksi melko selvä asia:
-
Jos ab
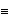 0 (mod p) ja p on
alkuluku, niin a
0 (mod p) ja p on
alkuluku, niin a 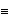 0 (mod p) tai b
0 (mod p) tai b 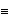 0 (mod p). Tämä päättely ei päde, kun p on koottu luku. Esimerkiksi 2·3
0 (mod p). Tämä päättely ei päde, kun p on koottu luku. Esimerkiksi 2·3 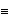 0 (mod 6), vaikka 2 > 0 ja 3
> 0.
0 (mod 6), vaikka 2 > 0 ja 3
> 0.
![]() b (mod p)
tarkoittaa, että p on a - b:n tekijä.
(Merkitään p | a - b.) Toisin sanoen, kun a tai b jaetaan p:llä;, saadaan sama
jakojäännös. Seuraavat alkeelliset laskusäännöt ovat voimassa (a,b mielivaltaisia kokonaislukuja, p > 0):
b (mod p)
tarkoittaa, että p on a - b:n tekijä.
(Merkitään p | a - b.) Toisin sanoen, kun a tai b jaetaan p:llä;, saadaan sama
jakojäännös. Seuraavat alkeelliset laskusäännöt ovat voimassa (a,b mielivaltaisia kokonaislukuja, p > 0):