[Matematiikkaa] [Edellinen: kertolaskua] [Valikkoon] [Etusivulle]

N-ulotteinen pallo

Huomautus: tästä aiheesta on verkossa olemassa n+1 dokumenttia, joita ei koskaan löydä kun pitäisi. Tämän sivun kirjoitin vain itselleni muistilapuksi.

Määritelmä: r-säteinen a-keskinen avoin pallo euklidisessa avaruudessa R^n on joukko

B_r(a) = { x \in R^n | norm( x - a ) < r }.

Suljettu pallo B*_r(a) saadaan korvaamalla määritelmässä < merkillä <=.

Tilavuus

Suuntaissärmiön tilavuus saadaan ottamalla determinantti matriisista, joka sisältää särmävektorit:

V = det( [a1 a2 ... an] ) = det( A ) = sqrt( det( A'A) ).

Mielivaltaisen kappaleen tilavuus saadaan sitten täyttämällä kappale differentiaalisen pienillä suuntaissärmiöillä ja summaamalla näiden tilavuudet. (Suomeksi: integroidaan.)

Pallon (suljettu tai avoin, sama se) tilavuus selviää integroimalla koordinaattiakselien suuntaisesti mitään ajattelematta alueen yli. Kun merkitään V^n(r) = a_n × r^n = r-säteisen pallon tilavuus R^n:ssä, saadaan yhtälö

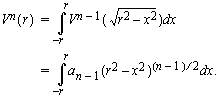
V^n(r) = Int( V^(n-1)( sqrt(r^2-x²) ), x = -r..r ) = a_(n-1)×Int( (r²-x²)^(n-1)/2, x = -r..r ).

Sijoittamalla x = r sin t ja pyörittämällä saadaan yhtälö

V^n(r) = (n-1)/n × a_(n-1)/a_(n-3) × r² × V^(n-2)(r),

josta edelleen

a_n = (n-1)/n × a_(n-1) a_(n-2)/a_(n-3) = (n-2)/n × (a_(n-2))²/a_(n-4).

Lisäksi tiedetään, että a2 = π, a3 = 4π/3, ja integraalista voi suoraan ratkaista kertoimen a4 = π²/2. Näiden avulla saisi sitten tuosta rekursiokaavasta kaikki loput kertoimet. Kun kaavaa vähän pyörittää, on helppo (eikä ole) nähdä kertoimien lausekkeet:

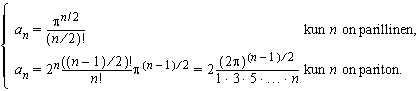
a_n = 1/(n/2)! × pi^(n/2), kun n on parillinen, a_n = 2^n/n! × ((n-1)/2)!× pi^((n-1)/2) = 2 × (2pi)^((n-1)/2)/(1×3×...×n), kun n on pariton.

Gammafunktion avulla saa parillisille ja parittomille kertoimille nätisti yhden ja saman kaavan. Kun

Gamma(n) = Int( t^(n-1) exp(-t), t = 0..Inf ),

niin

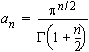
a_n = pi^(n/2) / Gamma( 1 + n/2 )

ja siten

V^n(r) = pi^(n/2) r^n / Gamma( 1 + n/2 ).

Vielä parin ensimmäisen pallon tilavuudet:

n 0 1 2 3 4 5 6 7
V^n(r) 1 2r πr² 4πr³/3 π²r4/2 8π²r5/15 π³r6/6 16π³r7/105
Kertoimen likiarvo 1.00000 2.00000 3.14159 4.18879 4.93480 5.26379 5.16771 4.72477
Edellinen | Matematiikan valikko | Etusivu
Mikko Pekkarinen, Sivu luotu 1999-03-01, muokattu 2000-11-14. URL: https://iki.fi/empii/matikka/pallo.html