Huomautus veneilijöille: Ikinä en ole lotonnut ensimmäistäkään ruudukkoa, niin että näiden vinkkien toimimattomuutta ei ole todettu käytännössä.
Kuten tunnettua, lotossa olisi tarkoitus arvata, mitkä 7 palloa niistä 39:stä sattuvat ulostautumaan siitä pesukoneesta. Eri mahdollisuuksia on
![]()
kappaletta. Jos oletetaan että vilppiä ei tapahdu, niin kukin yksittäinen rivi on yhtä todennäköinen. Myös todennäköisyys sille, että tietty pallo on mukana voittorivissä, on sama 7/39 kaikille palloille.
Tutkitaan nyt lottorivin numeroiden summaa, joka on seitsemän identtisesti jakautuneen satunnaismuuttujan summa. Keskeisestä raja-arvolauseesta seuraa, että tämä suure on likimain normaalisti jakautunut. Asia on helppo varmistaa laskemalla tietokoneella kaikki mahdolliset lottorivit ja niiden numeroiden summat.
Kuten kuvasta näkyy, jakautuma on todellakin likimain normaali.
Datasta on helppo laskea otoskeskiarvo ja
otoskeskihajonta: ![]()
(Asiaankuulumaton huomautus: yhdistelmältä Amstrad CPC 6128 & tulkattava Basic-ohjelma kului datan generoimiseen n. 58 tuntia. Vastaavasti 150Mhz Pentium ja C++-ohjelma suoriutui ajassa 4,3 sekuntia. Tietokoneiden suorituskyky on varmaan kasvanut viimeisen kymmenen vuoden aikana, tai jotain.)
Näin saatiin kivuttomasti tulos, jonka mukaan kannattaa veikata sellaisia rivejä, joissa numeroiden summa on 140. Ongelmaksi jää, että tällaisia rivejä on olemassa 219 489 kappaletta. Todennäköisyys osua oikeaan on edelleen melko pieni.
Lähestytään ongelmaa toiselta suunnalta. Kysymys kuuluu: millä todennäköisyydellä lottorivin p:nneksi pienin numero on arvoltaan k?
Tähän on onneksi helppo vastata. Vastaus on
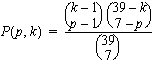
kun 1 ![]() p
p ![]() 7
ja p
7
ja p ![]() k
k
![]() p + 32.
Muussa tapauksessa todennäköisyys on nolla. Esimerkiksi ykkönen ei voi olla
rivin toiseksi pienin numero.
p + 32.
Muussa tapauksessa todennäköisyys on nolla. Esimerkiksi ykkönen ei voi olla
rivin toiseksi pienin numero.
![[Todennäköisyydet P(1,k), P(2,k), ..., P(7,k)]](../pictures/lotto-05.png)
Valitaan nyt lottorivin numerot siten, että pienin numero maksimoi P(1,k):n, toiseksi pienin maksimoi P(2,k):n jne. Näin saadaan poimittua kaikkien lottorivien joukosta neljä ehdokasta, sillä kaikki maksimit eivät ole yksikäsitteisiä.
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | Summa | |
|---|---|---|---|---|---|---|---|---|
| Rivi 1: | 1 | 7 | 13 | 20 | 26 | 33 | 39 | 139 |
| Rivi 2: | 1 | 7 | 13 | 20 | 27 | 33 | 39 | 140 |
| Rivi 3: | 1 | 7 | 14 | 20 | 26 | 33 | 39 | 140 |
| Rivi 4: | 1 | 7 | 14 | 20 | 27 | 33 | 39 | 141 |
Nämä ovat kiistattomasti todennäköisimmät lottorivit. Väitettä tukee sekin, että tulos on sopusoinnussa yllä saadun numeroiden summaa koskevan tuloksen kanssa.
Mitään edelläolevasta ei sitten kannata ottaa liian vakavasti.