Melkein kaikkialla jatkuva funktio

Tämä sivu on olemassa, koska näin oudon funktion olemassaolo ja seuraava todistus tekivät vaikutuksen joskus lukioaikana. Oikeastaan todistus ei ole hirmu ihmeellinen.

Väite: Seuraava yhden muuttujan funktio on jatkuva kaikissa irrationaalipisteissä, ja epäjatkuva, kun argumentti on rationaalinen:

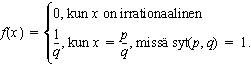
Edellä syt(p,q) tarkoittaa lukujen p ja q suurinta yhteistä tekijää. Ehto syt(p,q) = 1 sanoo vain, että murtolukua ei voi supistaa.

Funktion kuvaaja näyttää suunnilleen tältä:

Funktion f arvot, jotka ovat suurempia kuin 1/100 välillä (0,1]

Määritelmiä

• Funktion g: R R: x g(x) raja-arvo pisteessä p on L, jos
  
• Funktio g on jatkuva pisteessä p, jos raja-arvo tässä pisteessä on g( p ).
• Funktio on jatkuva, jos se on jatkuva jokaisessa pisteessä.

Väitteen todistus

Olkoon x irrationaalinen. Näytetään, että funktion f raja-arvo pisteessä x on olemassa ja arvoltaan 0. Valitaan mielivaltainen ε > 0 ja kokonaisluku Q siten että Q > 1/ε, jolloin 1/Q < ε.

[Laiska merkintä: Jatkossa kaikki rationaaliluvut oletetaan valmiiksi supistetuiksi, jolloin voi huoletta puhua rationaaliluvuista, joiden nimittäjä on jotain rajaa pienempi tai suurempi.]

Välin I = ( x - 1/2Q, x + 1/2Q ) pituus on 1/Q. Tähän väliin ei mahdu kahta rationaalilukua, joilla on sama nimittäjä q, jos 1 q Q, koskapa kahden tällaisen luvun erotus on vähintään 1/Q. Näinollen välissä I on tällaisia lukuja korkeintaan Q kappaletta; enintään yksi jokaista q:n arvoa kohti. Tästä äärellisestä joukosta voidaan poimia se luku r, joka on lähinnä pistettä x. Raja-arvon määritelmään kelpaa nyt deltaksi δ = | x - r |. Välin ( x - δ, x + δ ) kaikki rationaaliluvut ovat näet muotoa p/q, missä q > Q, jolloin f( p/q ) = 1/q < 1/Q < ε. Niinpä

eli raja-arvo on 0 = f( x ) ja f on tässä pisteessä jatkuva.

Samalla tavoin näytetään, että raja-arvo on nolla myös x:n rationaaliarvoilla. Siispä funktio f ei ole jatkuva missään pisteessä p/q.