Hianoin juttu näillä sivuilla. Ihan itse mietitty. Ei tätä kyllä kukaan jaksa lukea. Kärsimättömät siirtykööt suoraan sivun loppuun.
Säännöllinen monitahokas on kupera kappale, jonka tahkot ovat identtisiä säännöllisiä monikulmioita, ja jonka kärjet ovat keskenään samanlaisia. Kuperuus tarkoittaa, että kun valitaan kaksi pistettä kappaleen sisältä tai pinnalta, pisteiden yhdysjana on kokonaan kappaleen sisällä. Ehto kärkien samanlaisuudesta puolestaan sanoo, että esim. sellainen kappale, joka on saatu länttäämällä kaksi 5-kulmiopohjaista pyramidia pohjat vastakkain, ei ole säännöllinen. Jatkossa tarvitaan Eulerin monitahokaskaavaa, jonka mukaan
K + T = S + 2,
missä K, T ja S ovat kappaleen kärkien, tahkojen ja särmien lukumäärät. Kaava pätee mielivaltaiselle monitahokkaalle, mikä on melko helppo todistaa, jos sitä ei tarvitse tehdä itse. Tästä kaavasta lähtien on niinikään helppo näyttää, että säännöllisiä monitahokkaita on olemassa tasan viisi erilaista. Ne on esitetty kuvassa 1.
![[Säännölliset monitahokkaat]](../pictures/platon.png)
|
| Kuva 1. Platonin monitahokkaat: tetraedri, kuutio (eli heksaedri), oktaedri, dodekaedri ja ikosaedri. |
|---|
Sitten puolisäännöllisten monitahokkaiden kimppuun. Arkhimedes todisti, että tällaisia kappaleita on olemassa 13 kappaletta.[1] Tätä riviä kirjoittaessa puolisäännöllisen monitahokkaan tarkka määritelmä ei ole tiedossani. Tämän seurauksena sivun rakenne on hieman takaperoinen. Yritetään löytää 13 kappaletta sekä järkevä määritelmä, jonka perusteella ne voi löytää. Ensimmäinen (epätäydellinen) yritelmä: Puolisäännöllinen monitahokas on kupera kappale, jonka tahkot ovat säännöllisiä monikulmioita (eivät kaikki samanlaisia), ja jonka kärjet ovat keskenään identtisiä. (Oikeastaan tämä on melkein oikea määritelmä.)
Helppo tapa löytää muutama puolisäännöllinen monitahokas on leikellä säännöllisten tahokkaiden kulmia. Esimerkiksi kuutiosta saa kaksi erilaista puolisäännöllistä monitahokasta (kuva 2).
![[Puukotettu kuutio]](../pictures/cube.png)
|
| Kuva 2. Kaksi tapaa leikata kuutiosta kulmat. |
|---|
Seuraavassa taulukossa on lueteltu kaikki tällä tavoin saatavat kappaleet.
| Perusmuoto | Ensimmäinen leikkaus | Toinen leikkaus |
|---|---|---|
| Tetraedri | 4 kolmiota, 4 6-kulmiota. |
4 kolmiota, 4 kolmiota. oktaedri, säännöllinen. |
| Kuutio | 8 kolmiota, 6 8-kulmiota. |
8 kolmiota, 6 neliötä. |
| Oktaedri | 6 neliötä, 8 6-kulmiota. |
6 neliötä, 8 kolmiota. sama kuin yllä. |
| Dodekaedri | 12 10-kulmiota, 20 kolmiota. |
12 5-kulmiota, 20 kolmiota. |
| Ikosaedri | 20 6-kulmiota, 12 5-kulmiota. |
20 kolmiota, 12 5-kulmiota. sama kuin yllä. |
Näin saatiin seitsemän kappaletta, mikä ei vielä riitä. Haetaan seuraavaksi ratkaisua systemaattisemmin. Tarkastellaan monitahokkaan yhtä kärkeä. Leikataan yksi kärkeen tuleva särmä auki, ja levitetään kärkeä ympäröivät sivutahkot tasoon (kuva 3).
![[Viisi tasasivuista kolmiota, yhteensä 300°C]](../pictures/taso.png)
|
| Kuva 3. Kuperan tahokkaan kärjissä oleva kulma on täyttä kulmaa pienempi. |
|---|
Kärjessä muodostuvan kulman tulee olla alle 360°. Jos kulma olisi tasan 360 astetta, kyseessä olisi tasokuvio, ja suuremmasta kulmasta aiheutuisi taas kupru. (Yritä liimata kasaan pyramidi, jonka sivuina on 7 tasasivuista kolmiota. Ei onnistu.) Jatkoa ajatellen on hyvä tietää, että säännöllisen n-kulmion kulman suuruus on
180° - 360°/n = 180°( 1 - 2/n ).
Oletetaan, että kappale koostuu säännöllisistä m- ja n-kulmioista siten, että yhdessä kärjessä kohtaa aina p kappaletta m-kulmioita ja q kappaletta n-kulmioita. Edellisen nojalla saadaan epäyhtälö
p( 1 - 2/m ) + q( 1 - 2/n ) < 2.
Mahdollisia monitahokaskandidaatteja ovat kaikki ne, jotka toteuttavat tuon epäyhtälön. Siispä ensin on löydettävä yhtälön kaikki kokonaislukuratkaisut. Ne on lueteltu alla. (Taulukossa m < n. Turha niitä on kahdesti luetella eri nimillä.)
|
|
|
Lisäksi löytyy kolme ääretöntä tapausta, jotka tuosta puuttuvat:
Kuten fiksumpi melko helposti huomaa, noita vaihtoehtoja oli yli 13, joten ne eivät kaikki voi kelvata. Riittävästi lisäehtoja saadaan Eulerin kaavasta. Merkitään kappaleen m-kulmioiden määrää a:lla ja n-kulmioiden määrää b:llä. Selvästi tahkoja on yhteensä T = a + b kappaletta. Sivutahkoilla on sivuja yhteensä am + bn kappaletta, ja koska kullakin monitahokkaan särmällä kahden tahkon sivut kohtaavat, särmiä on yhteensä S = ( am + bn )/2 kappaletta. Kärkien määrän voi päätellä samoin: sivutahkoilla on yhteensä am + bn kulmaa. Kussakin tahokkaan kärjessä kohtaa p + q tahkoa, joten kärkiä on yhteensä K = ( am + bn )/( p + q ) kappaletta. Toisaalta m-kulmion kulmia on yhteensä am kappaletta, ja joka kärkeen näitä riittää p kappaletta, joten K = am/p. Vastaavasti myös bn/q = K. Sijoittamalla K, S ja T Eulerin kaavaan ja merkitsemällä K:n eri esitysmuodot yhtäsuuriksi, tuloksena on yhtälöpari, josta a ja b voidaan ratkaista:
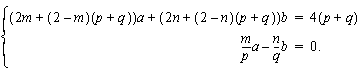
Hoidetaan ensin tieltä pois yllä listatut kolme erikoistapausta.
![[Sirkusjakkara ja 5-kulmiopohjainen särmiö]](../pictures/sarmio.png)
|
| Kuva 4. a) Kaksi n-kulmiota ja 2n kolmiota, b) kaksi n-kulmiota ja n neliötä. |
|---|
Jos ja kun halutaan löytää äärellinen määrä kappaleita, nuo särmiöt pitää hylätä. Määrätään, että puolisäännöllisessä monitahokkaassa on kutakin muotoa olevia tahkoja vähintään kolme kappaletta.
Sitten on seulottava jäljelläolevat 23 tapausta. Alla on yhtälöparin ratkaisu kaikissa tapauksissa. Merkintä '/' tarkoittaa, että saadut tahkomäärät eivät ole kokonaislukuja, ja '-' merkitsee, että ratkaisua ei ole olemassakaan.
|
|
Tässä vaiheessa ehdokkaita on vielä mukana 17 kappaletta, joista numero 1 hylätään heti kättelyssä, koska se on särmiö. Tutkitaan nyt kappaletta numero 21. Sen kussakin kärjessä kohtaa kaksi 5-kulmiota ja 8-kulmio. Tarkastellaan yhtä 5-kulmiota (kuva 5). On mahdotonta, että sen kahdella vierekkäisellä sivulla olisi samanmuotoiset tahkot. Jos näin olisi, muodostuisi monitahokkaaseen kärki, jossa kohtaa kolme 5-kulmiota, tai kärki, jossa kohtaa kaksi 8-kulmiota ja 5-kulmio. Siispä 5-kulmion kahden vierekkäisen sivun naapureina on aina erimuotoiset tahkot. Tästä seuraa kuitenkin heti ristiriita, koska viisi on pariton luku (katso kuvaa).
![[5-kulmio 5- ja 8-kulmioiden keskellä.]](../pictures/5kulmio.png)
|
| Kuva 5. Miten valita 5-kulmion sivuista joka toinen? Ei mitenkään. |
|---|
Näinollen ehdokas 21 ei voi olla kelvollinen puolisäännöllinen monitahokas. Samalla päättelyllä voidaan hylätä muutkin sellaiset ehdokkaat, joiden yhdessä kärjessä kohtaa kaksi pariton-kulmiota ja yksi x-kulmio. Tällaisia ovat ehdokkaat 7, 9, 16, 19 ja 22. Jäljelle jää 10 monitahokasta, jotka kaikki kelpaavat. Seitsemän näistä kymmenestä oli jo mukana taulukossa 1, jossa lueteltiin säännöllisiä monitahokkaita silpomalla saadut tuotokset.
Olettaen, että löydetyt 10 ovat todellakin puolisäännöllisiä monitahokkaita, löytämättä on vielä kolme kappaletta. Koska kahden erilaisen tahkon tapaus on nyt loppuunkäsitelty, täytyy etsiä kappaleita, joilla on kolmenlaisia sivutahkoja. Kappaleita, joiden tahkot olisivat neljää tai useampaa eri sorttia, ei ole olemassa. Tämä nähdään käyttämällä ehtoa, jonka mukaan kärjessä kohtaavien kulmien summa on alle 360°. Neljällä erimuotoisella monikulmiolla tämä summa on vähintään 60° + 90° + 108° + 120° = 378°.
Olkoon monitahokkaassa a kappaletta m-kulmioita, b kappaletta n-kulmioita ja c kappaletta o-kulmioita, ja kussakin kärjessä kohdatkoon p m- kulmiota, q n-kulmiota ja r o-kulmiota. Kuten kahden erimuotoisen tahkon tapauksessa yllä, haetaan ensin kaikki sellaiset kokonaislukukolmikot ( m, n, o ) ja ( p, q, r ), jotka täyttävät kulmaehdon
![]()
Osoittautuu, että ratkaisuja on 93 kappaletta, ja lisäksi vielä kolme sellaista ratkaisua, joissa max( m, n, o ) saa olla mitä vaan. Tämä on hieman liikaa, joten karsitaan enemmistö pois jo ennen eri vaihtoehtojen luettelemista. Näytetään, että kun p = q = r = 1 ja m, n tai o on pariton, tuloksena ei ole mitään järkevää. Päättely on ihan sama kuin aiemmin. Valitaan pariton-kulmio. Sen ympärillä olevat tahkot ovat kaikki niitä kahta muuta muotoa, ja vieläpä vuorotellen. Kuten nähtiin, ei pariton- kulmiota voi ympäröidä vuorotahdilla, joten moisia kappaleita ei ole.
Jäljelle jää 12 vaihtoehtoa, mikä on jo inhimillisempää. Muodostetaan nyt tahkojen, särmien ja kärkien lukumäärien lausekkeet. Näin saadaan yhtälöryhmä, josta a, b ja c ratkeavat:
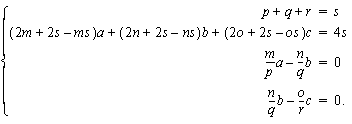
Ratkaisut ovat seuraavassa taulukossa. Kuten aiemminkin, '/' tarkoittaa, että kyseessä on murtoluku ja vastaus ei kelpaa.
| (m,n,o) | (p,q,r) | (a,b,c) | |
|---|---|---|---|
| 1 | (3,4,5) | (2,1,1) | (/,/,/) |
| 2 | (3,4,6) | (2,1,1) | (16,6,4) |
| 3 | (3,4,7) | (2,1,1) | (/,/,/) |
| 4 | (3,4,8) | (2,1,1) | (32,12,6) |
| 5 | (3,4,9) | (2,1,1) | (48,18,8) |
| 6 | (3,4,10) | (2,1,1) | (80,30,12) |
| 7 | (3,4,11) | (2,1,1) | (176,66,24) |
| 8 | (3,5,6) | (2,1,1) | (40,12,10) |
| 9 | (3,5,7) | (2,1,1) | (140,42,30) |
| 10 | (3,4,5) | (1,2,1) | (20,30,12) |
| 11 | (4,6,8) | (1,1,1) | (12,8,6) |
| 12 | (4,6,10) | (1,1,1) | (30,20,12) |
Kelvollisia ehdokkaita löytyi kymmenen. Näistä pitäisi nyt hylätä seitsemän. Tutkitaan ensin kappaletta 2. Joka kärjessä kohtaa kaksi kolmiota, neliö ja kuusikulmio. Valitaan mielivaltainen kolmio. Sen kaikki naapurit ovat keskenään erilaisia, koska muutoin muodostuisi laiton kärki (kaksi neliötä, kaksi 6-kulmiota tai kolme kolmiota samassa kärjessä). Jokaisella kolmiolla on siis yksi yhteinen sivu neliön kanssa. Neliön sivuja on yhteensä 24, joista kolmioiden kanssa yhteisiä on 16. Tämä on ristiriita, sillä neliöitä on kuusi kappaletta ja niillä kaikilla pitäisi olla identtiset naapurit, mutta 16 ei ole jaollinen kuudella. Samalla perusteella voidaan hylätä ehdokkaat 4 ja 6.
Otetaan käsittelyyn ehdokas 8: kussakin kärjessä kohtaa kaksi kolmiota, 5-kulmio ja 6-kulmio. Tutkitaan 5-kulmiota. Jos sillä on naapurina 6-kulmio, pitää joka toisen naapurin olla 6-kulmio, jotta kärjet olisivat keskenään identtisiä. Tämä on nähty mahdottomaksi jo moneen kertaan, joten kaikki 5-kulmion naapurit ovat kolmioita. Jotta kärjet 5-kulmion ympärillä olisivat laillisia, pitää kolmioiden välissä olla 6-kulmiot (kuva 6). Tästä seuraa kuitenkin laittomat kulmat kolmioiden kärkiin, joten ehdokas on hylättävä. Samoin voidaan hylätä muut ehdokkaat, joiden kärjissä kohtaa 2 kolmiota, 1 pariton-kulmio ja 1 x-kulmio. Tällaisia ovat ehdokkaat 5, 7 ja 9. Jäljelle jäävät 10, 11 ja 12: juuri haluttu määrä.
![[5-kulmio kolmioiden keskellä. Minne 6-kulmiot?]](../pictures/5kulmio2.png)
|
| Kuva 6. Kun kärjet A ja B ovat oikein, kärki C menee väärin. |
|---|
Edellä löydettiin kaikki 13 puolisäännöllistä monitahokasta. Tässä kohdin huijataan sen verran, että löydösten kelpaaminen jää uskon ja kuvien varaan. Edellisen esityksen perusteella mikään ei vielä takaa, että jäljellejääneet ehdokkaat olisivat ihan oikeita monitahokkaita.
Seuraavassa taulukossa on vielä kertaalleen lueteltu kaikki kolmetoista kappaletta. Mukana on myös kappaleiden kärkien, tahkojen ja särmien lukumäärät. Kärkien lukumäärän jälkeen suluissa lukee kussakin kärjessä kohtaavien tahkojen kulmien määrät.
| Kuva | Kärkiä | Särmiä | Tahkoja | Muuta |
|---|---|---|---|---|
![[Kuva]](../pictures/solid02.png) |
24 (3,4,4,4) | 48 | 26 (8 kolmiota ja 18 neliötä) | Vuonna 1 ja 2 Rubikin madosta tehtiin tällaisia. |
![[Kuva]](../pictures/solid04.png) |
12 (3,6,6) | 18 | 8 (4 kolmiota ja 4 6-kulmiota) | Saadaan tetraedrista leikkaamalla kulmat. |
![[Kuva]](../pictures/solid06.png) |
24 (3,8,8) | 36 | 14 (8 kolmiota ja 6 8-kulmiota) | Kuutiosta. |
![[Kuva]](../pictures/solid08.png) |
60 (3,10,10) | 90 | 32 (20 kolmiota ja 12 10-kulmiota) | Dodekaedrista. |
![[Kuva]](../pictures/solid10.png) |
12 (3,4,3,4) | 24 | 14 (8 kolmiota ja 6 neliötä) | Kuutiosta tai oktaedrista. |
![[Kuva]](../pictures/solid11.png) |
30 (3,5,3,5) | 60 | 32 (20 kolmiota ja 12 5-kulmiota) | Dodekaedrista tai ikosaedrista. |
![[Kuva]](../pictures/solid12.png) |
24 (3,3,3,3,4) | 60 | 38 (32 kolmiota ja 6 neliötä) | Tein Lappari-tölkeistä tämänmuotoisen lampunvarjostimen. Hieno. Toinen niistä kahdesta kappaleesta, jotka eivät ole peilisymmetrisiä. |
![[Kuva]](../pictures/solid13.png) |
60 (3,3,3,3,5) | 150 | 92 (80 kolmiota ja 12 5-kulmiota) | Koko tämän kirjoituksen alkuunpanija. Näin joskus aikoinaan Heurekassa tämänmuotoisen peilipallon. Tämäkään ei ole peilisymmetrinen. |
![[Kuva]](../pictures/solid15.png) |
24 (4,6,6) | 36 | 14 (6 neliötä ja 8 6-kulmiota) | Saadaan leikkaamalla oktaedrin kulmat. |
![[Kuva]](../pictures/solid18.png) |
60 (5,6,6) | 90 | 32 (12 5-kulmiota ja 20 6-kulmiota) | Ikosaedrista. C-60 molekyyli tai jalkapallo. |
![[Kuva]](../pictures/solid30.png) |
60 (3,4,5,4) | 120 | 62 (20 kolmiota, 30 neliötä ja 12 5-kulmiota) | Saadaan räjäyttämällä dodekaedri ja täyttämällä raot neliöillä ja kolmioilla. |
![[Kuva]](../pictures/solid31.png) |
48 (4,6,8) | 72 | 26 (12 neliötä, 8 6-kulmiota ja 6 8-kulmiota) | Saadaan leikkaamalla kuutiosta kärjet ja särmät. Vaihtoehtoisesti räjäyttämällä viides puolisäännöllinen. |
![[Kuva]](../pictures/solid32.png) |
120 (4,6,10) | 180 | 62 (30 neliötä, 20 6-kulmiota ja 12 10-kulmiota) | Neljäs puolisäännöllinen räjäyttämällä. |