Mikä tämä on?

Kuva 1: Liian paksu ympyräksi.

Tällaisen kuvion olen nähnyt useammassakin paikassa; ainakin yläasteen matikankirjassa sekä yhdessä Amiga Basick -demossa. Elin pitkään siinä luulossa, että reunaviiva muodostaa ympyrän, mutta kyllähän tuosta näkee silmälläänkin, että kuvio on liian pullea ympyräksi. Joten mikä kuvio tuohon keskelle sitten muodostuu, kun suorien määrän annetaan kasvaa rajatta?

Kuva 2: Kuvion neljännes lähikuvassa.

Keskitytään tutkimaan kuvion yhtä neljännestä (Kuva 2). Reunakäyrän yhtälö on helppo johtaa epäelegantisti. Valitaan kaksi suoraa, jotka leikkaavat x-akselin pisteissä t ja t + Δt. Kirjoitetaan näiden suorien yhtälöt, ja ratkaistaan piste, jossa suorat leikkaavat. Haettu käyrä kulkee likimain tämän pisteen kautta. Kun annetaan sitten Δt:n mennä nollaksi, saadaan etsityn käyrän yhtälö muodossa x = x( t ), y = y( t ). Asian voi kuitenkin tehdä kauniimmin, ja samalla vaivalla saadaan yleisempi tulos.

Teoreettista lätinää

Esittäköön f( x, c ) yksiparametrista käyräparvea. Tämä tarkoittaa, että kutakin c:n arvoa c₀ vastaa oma käyränsä y = f( x, c₀ ). Nyt pitäisi löytää käyrä x = x( t ), y = y( t ), joka kaikilla t:n arvoilla sivuaa yhtä annetun parven käyrää. Tällaista otusta kutsutaan verhokäyräksi. Oletetaan, että funktio f on jatkuvasti derivoituva kummankin argumenttinsa suhteen. Suomeksi sanottuna kukin parven käyristä on sileä, ja kun c:n arvoa vähän muutetaan, niin käyräkin liikahtaa vain vähän. Lisäksi joudutaan olettamaan, että funktio c( t ) ei ole vakio missäänpäin t:n arvoaluetta. (Funktio c( t ) kertoo mitä parven käyristä sivutaan milläkin t:n arvolla. Tätä ei tunneta. Jos c( t ) olisi vakio jossain alueessa, niin haettu käyrä sivuaisi useaa käyräparven f käyrää yhdessä pisteessä. )

Sivuamispisteessä verhokäyrän ja sivutun käyrän kulmakertoimet ovat samat, ja lisäksi tietenkin sivuamispiste on käyrille yhteinen. Näistä ehdoista saadaan yhtälöpari

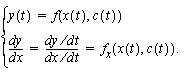
Molemmat yhtälöt ovat t:n suhteen identiteettejä, eli ne pätevät kaikilla t:n arvoilla. Derivoimalla ensimmäinen yhtälö puolittain t:n suhteen saadaan

Kun tämän sijoittaa yhtälöparin alempaan yhtälöön, niin terve näkee että

Jotta tämä pitäisi paikkansa, riittää että tulon ensimmäinen tekijä on nolla. Tämä on myös välttämätön ehto, sillä oletettiin, että c( t ) ei ole vakio. Verhokäyrän yhtälö voidaan (jos voidaan) nyt ratkaista muodossa x = x( c ), y = y( c ) yhtälöparista

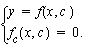
Jos lisäksi , niin implisiittifunktiolause sanoo, että jälkimmäisestä yhtälöstä ratkeaa c( x ), jolloin verhokäyrälle saadaan yhtälö y = g( x ) = f( x, c( x ) ).

Alkuperäinen ongelma

Käytetään yllä saatua tulosta nyt alkuperäiseen ongelmaan. Kaukaa viisaasti käännetään ensin koordinaatistoa 45°, ja ratkaistaan samalla vaivalla yleisempi tapaus, jossa akselit eivät ole toisiaan vastaan kohtisuorassa (Kuva 3).

Kuva 3: Suorarykelmä jossa akselit eivät ole kohtisuorassa.

Suoraparvea esittää nyt yhtälö

Tämän derivaatta c:n suhteen on

Kun tuo merkitään nollaksi ja ratkaistaan c, tuloksena on

Verhokäyrän yhtälö on siten

Kyseessä on siis paraabeli. Kuvassa 1 on siten neljä paraabelin kaarta, eikä mikään ympyrä.